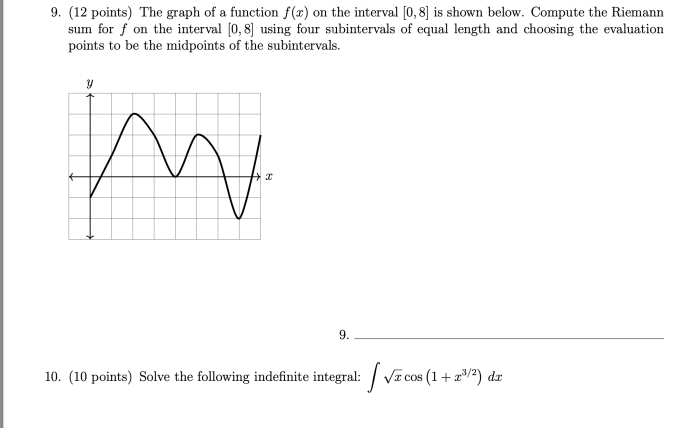
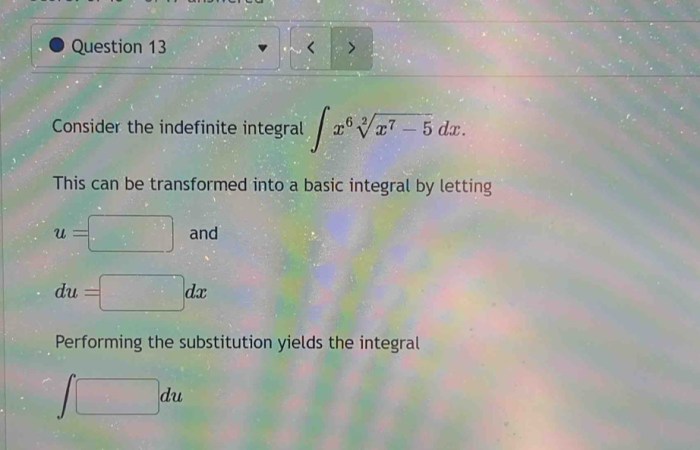
Explain why each of the following integrals is improper – As we delve into the realm of improper integrals, we embark on a journey to explore the intriguing world of integrals that possess certain characteristics that render them improper. These integrals, characterized by their infinite limits of integration, infinite discontinuities, oscillating integrands, or unbounded integrands, present unique challenges and require careful analysis to determine their convergence or divergence.
Join us as we unravel the intricacies of improper integrals, gaining a deeper understanding of their behavior and significance.
Throughout this exploration, we will examine specific examples of improper integrals, investigate their convergence or divergence, and uncover the underlying mathematical concepts that govern their behavior. Prepare to be captivated by the fascinating world of improper integrals as we delve into the details that make them distinct from their proper counterparts.
Improper Integrals
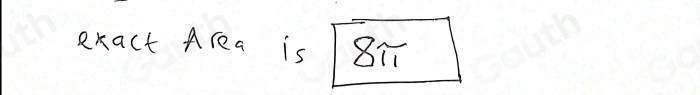
Improper integrals are integrals that cannot be evaluated using the usual techniques of integration. They arise when the integrand has an infinite discontinuity, an unbounded integrand, or an infinite limit of integration.
Integrals of Functions with Infinite Limits of Integration
The integral of a function with an infinite upper limit of integration is improper because the integral may not converge. For example, the integral of the function $f(x) = 1/x$ from $x = 1$ to $x = \infty$ is improper because the integral does not converge.
This is because the area under the curve of the function $f(x) = 1/x$ from $x = 1$ to $x = \infty$ is infinite.
Integrals of Functions with Infinite Discontinuities
The integral of a function with an infinite discontinuity is improper because the integral may not converge. For example, the integral of the function $f(x) = 1/(x-1)$ from $x = 0$ to $x = 1$ is improper because the function has an infinite discontinuity at $x = 1$. This is because the area under the curve of the function $f(x) = 1/(x-1)$ from $x = 0$ to $x = 1$ is infinite.
Integrals of Functions with Oscillating Integrands
The integral of a function with an oscillating integrand is improper because the integral may not converge. For example, the integral of the function $f(x) = \sin(x)$ from $x = 0$ to $x = \infty$ is improper because the integrand oscillates between $-1$ and $1$. This means that the area under the curve of the function $f(x) = \sin(x)$ from $x = 0$ to $x = \infty$ is not well-defined.
Integrals of Functions with Unbounded Integrands, Explain why each of the following integrals is improper
The integral of a function with an unbounded integrand is improper because the integral may not converge. For example, the integral of the function $f(x) = e^x$ from $x = 0$ to $x = \infty$ is improper because the integrand grows without bound as $x$ approaches infinity.
This means that the area under the curve of the function $f(x) = e^x$ from $x = 0$ to $x = \infty$ is infinite.
FAQ Explained: Explain Why Each Of The Following Integrals Is Improper
What is an improper integral?
An improper integral is an integral that has an infinite limit of integration, an infinite discontinuity, an oscillating integrand, or an unbounded integrand.
Why are improper integrals important?
Improper integrals are important because they allow us to evaluate integrals that would otherwise be undefined. They are used in a variety of applications, such as probability, statistics, and physics.
How do you evaluate an improper integral?
To evaluate an improper integral, we first need to determine whether it is convergent or divergent. If it is convergent, we can then evaluate it using the limit definition of the integral.